Teooria
2007. aastal külastasin Tallinnas Robotex’i võistlust. Pärast üritust bussiga Tartu poole sõites helises minu taga ühe noorhärra telefon. Ilmselt küsiti tema muljeid Robotex’i kohta, sest ta vastas: “Nägin päris palju tudengeid, kes olid olnud vähemalt kaks ööpäeva magamata.”
Mis on siin oluline?
- Tudengid on piisavalt tarkust kogunud ja tunnetavad, et ülesanne on neile jõukohane;
- Nad on nõus panustama oluliselt aega parema tulemuse saavutamise nimel;
- Nad arvestavad sellega, et midagi on vaja juurde õppida;
- Nad on valmis meeskonnatööks.
Igapäevase õppetöö kontekstis võib väita, et tudengitele tuleb püstitada põnevad iseseisva töö ülesanded, mis on nende teadmiste ja mitteteadmiste piirimail, ning tekitada lahendajate vahel positiivne konkurents.
Jõudmaks tehnilise loovuseni, on kõigepealt vaja õppida. Tehnilises hariduses peab omama ülevaadet tehnoloogilisest maailmapildist ning valemite-jooniste keeltest, millega seda kirjeldatakse. Loovuse tulemus avaldub siin esmajoones uue ja vajaliku idee või asja väljapakkumises või ka tootmisprotsessi moderniseerimises. Päriselus annab loovustegevusele tagasiside näiteks patendiamet, retsenseerimine või idee realiseerimisest saadav majanduslik kasum. Õppeprotsessis on tagasiside andmise kohustus õppejõul ja sellel on määrav tähtsus õppurite loova tegevuse motiveerimisel. Õppejõud valib, kas parima hinde saab tudeng, kes suudab eksamil täpselt ette kanda loengus esitatud materjali, või tudeng, kes õppimise käigus demonstreerib iseseisva loova mõtlemise oskust.
Praktika
Tartu Ülikooli loodus- ja tehnoloogiateaduskonna kursustes “Insenerigraafika I” ja “… II” lähtun iseseisvate tööde koostamisel järgmisest ajalise järgnevuse loogikast:
- I kursus – tehnilise õppimise ülesanded, loovusega seotud ülesanded, tehnilise õppimise ülesanded;
- II kursus – tehnilise õppimise ülesanded, individuaal- ja meeskonnatöö loovusega seotud ülesanded.
Tehnilise õppimise tulemusena peab üliõpilane esimese kursuse lõpuks oskama koostada 15–25 mõõdet sisaldavast detailist tema valmistamiseks vajaliku joonise, mis sisaldab vajaliku arvu vaateid ja lõikeid ning kõik vajalikud mõõtmed. Teise kursuse lõpuks peab üliõpilane oskama vormistada mudelite koostusid ja koostejooniseid, mis sisaldavad iste ja tolerantse.
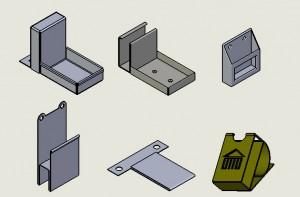Loovusülesannete korral on formuleeritud lõpptulemus ja lahenduskäiku piiravad tingimused. See tähendab, et ülesandepüstitusse on sihilikult sisse jäetud vabadusastmed, kus lahendaja peab ise otsustama, millist teed mööda jõuda lõpptulemuseni. Tudengite otsustusjulguse motiveerimiseks rõhutan, et ülesandel on mitu erinevat, kuid õiget lahendust. Näiteks tuleb Solidworks’i tarkvaraga voltida plekist tikutopsihoidja, millest inimene saab ühe käega võta tikku ja selle põlema tõmmata (erinevad lahendid on toodud kõrvaloleval pildil), või grupitööna modelleerida lapsele 40-liitrilise mahuga käru mänguasjade vedamiseks.
Individuaalsed tööd esitavad tudengid Blackboard’i vahendusel ja sealt näevad nad oma konkreetsele tööle pandud hinnet (punkte) ja kommentaare. Loengu alguses kommenteeritakse tööde eest pandud punktide jaotust. Tänu sellele saab iga tudeng positsioneerida end kogu grupi suhtes: kas tema esitatud töö kuulub paremate või tagasihoidlikumate hulka. Järgnevalt näidatakse parimaid lahendeid, nimetades ära nende autorid ja selgitades, miks töö väärib esiletõstmist. Parimatele töödele lisatakse ka preemiapunktid. Töödes esinevad korduvad vead analüüsitakse ilma konkreetsete tööde autoreid välja toomata.
Kokkuvõte
Selliseid loovust toetavaid ülesandeid ja hindamise skeemi olen kasutanud viimased viis aastat ja ÕISi tagasiside põhjal tudengid aktsepteerivad seda. Mitte rohkem kui üks-kaks tudengit sajast on tulnud hiljem küsima, miks nende töö on teeninud vähem punkte kui loodetud.
Peeter Kukk
